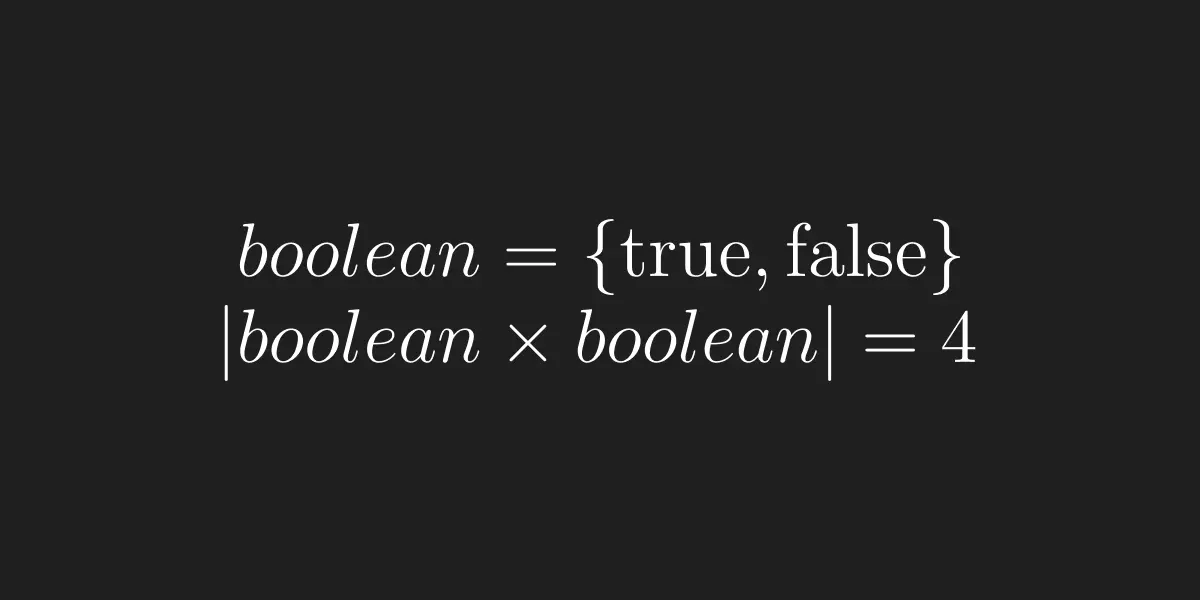Introduction#

Algebraic data types are types that are often used by millions of developers every day. In fact as time goes on, more and more languages are adopting algebraic data types as a core feature. There's no better time than the present to learn about them.

A Soft Introduction to Type Theory#

Type theory is simply a formal way of defining types. You can think of it to be similar to runtime analysis, but for types.

I first want to show you that a type can be expressed as a set of all it's possible values. For example, the type boolean can be represented like so:

A char could be represented as (assuming it's a-z):

Again, because a char can only be one of the letters in the alphabet from a-z.

This representation is useful because it gives us a structured way to model types. For example, if we ask ourselves, "is true assignable to boolean? We simply see if $\text{true} \in \text{boolean}$ holds. On the contrary, if we ask ourselves, "is 1 assignable to boolean? We can see that $\text{1} \notin \text{boolean}$ holds. Neat!

In the next few sections I'll discuss some properties of these sets and how they are presented in Java¹.

Sum Types#

Things with algebraic data types get interesting when we start to apply operations to them. Let's start with a simple example.

Given an enum:

enum Color {
  RED,
  GREEN,
  BLUE
}

We can represent the type Color as:

As Color can only be RED, GREEN, or BLUE. Note how it can't be two of these at the same time. Let's count the number of possible values for Color. We can do this by counting the number of elements in the set:

If we add another color to Color, say YELLOW, then the set of all possible values for Color would be:

By now, you should see a very clear pattern, the number of possible types for Color is the number of enum variants it has. In other words, if we take the sum of the number of variants in an enum, we get the number of possible types for that enum. Because of this, enums are known as sum types. In fact booleans are sum types too! Recall $|\text{boolean}| = 2$, and there are two variants for boolean, true and false. therefore boolean is a sum type.

Properties of Sum Types#

Sum types exhibit certain properties that make them useful for developers. Let's go over them.

Exhaustiveness#

Sum types are exhaustive, this both the developer and compiler able to make sure all variants are handled. For example, if we implement toString for Color like so using the new switch expression syntax²:

  @Override
  public String toString() {
    return switch (this) {
      case RED -> "Red";
      case GREEN -> "Green";
      case BLUE -> "Blue";
    };
  }

We can be sure that all variants of Color are handled. If we add a new variant to Color, say YELLOW, the compiler will complain that YELLOW is not handled in the switch statement:

  @Override
  public String toString() {
    return switch (this) { // Compiler error: Switch case YELLOW not handled
      case RED -> "Red";
      case GREEN -> "Green";
      case BLUE -> "Blue";
    };
  }

This makes our code much safer and forces us to handle all variants.

Uniqueness#

Each constituent of a sum type is unique. For example, Colors.RED is not Colors.GREEN, and Colors.GREEN is not Colors.BLUE. Additionally, Colors cannot take on multiple variants at the same time. It cannot be Colors.RED and Colors.GREEN at the same time. Because of this we say that sum types are disjoint.

Product Types#

So far we've only looked a types that take on one value at a time. Let's look at a type that can take on multiple values at the same time. Here's a more complex type, a tuple record with two fields:

record Container(bool foo, bool baz) {}

Unlike the sum types we've seen so far, Container can be multiple types at the same time. It can be foo=true, bar=true, foo=true, bar=false, foo=false, bar=true, or foo=false, bar=false. What's the set of all possible types for Container? Well, we can represent it as:

Notice something interesting? The set of all possible values for Container is the cartesian product of the set of all possible values for boolean with itself. We could also represent Container as a product of two booleans:

By this, we can assume that if another field boolean baz was added to Container (Containter(bool, bool, bool)), the set of all possible values for Container would be $\text{boolean} \times \text{boolean} \times \text{boolean}$.

Container is known as a product type for this specific reason, the set of types it represents is the product of the types it's composed of. However, if we want to be more specific we can say that Container is a product of sum types. This is because boolean is a sum type, and Container is a product of booleans.

Properties of Product Types#

Composability#

Product types are composable. This means that we can compose product types to create even more complex types.

If we create refer back to the Color example, we can compose Color with Container to create a new type ColorContainer:

record ColorContainer(Color color, Container container) {}

We can represent the set of all possible values for ColorContainer as:

Pretty complex set of possible values right? While this may be unneccearily complex, it's helps us understand even in the most complex cases, product types are still composable.

The problem with open types#

An open³ type can be thought of as a type that can be extended or implemented by any data structure. For example, in Java, class can implement the Iterator<T> interface. Consider a Java interface defined like so:

interface Animal {
  String name();
  int age();
  String sound();
}

We'll then add some variants:

record Dog(String name, int age, String sound) implements Animal {
  public Dog(String name, int age) {
    this(name, age, "Woof");
  }
 
  public void walk() {
    System.out.println("Walking " + this.name());
  }
}
 
record Cat(String name, int age, String sound) implements Animal {
  public Cat(String name, int age) {
    this(name, age, "Meow");
  }
 
  public void cleanLitterBox() {
    System.out.println("Cleaning litter box for " + this.name());
  }
}
 
record Cow(String name, int age, String sound) implements Animal {
  public Rhino(String name, int age) {
    this(name, age, "Moo");
  }
}

I now have a new requirement I want to model Animals that can be house pets. So now I'll introduce a new interface:

interface HousePet extends Animal {
  default void takeCareOf() {
    System.out.println("Taking care of " + this.name());
  }
}

I'll then make sure Dog and Cat implement HousePet:

- record Dog(String name, int age, String sound) implements Animal
+ record Dog(String name, int age, String sound) implements HousePet
- record Cat(String name, int age, String sound) implements Animal
+ record Cat(String name, int age, String sound) implements HousePet

This is great! I can now use a constraint to handle cases specifically for HousePets:

void takeCareOfHousePets(List<HousePet> animals) {
  for (Animal animal : animals) {
    animal.takeCareOf();
  }
}

I also need to handle specific tasks for each kind of HousePet, so I do this:

void takeCareOfHousePets(List<HousePet> animals) {
  for (Animal animal : animals) {
    if (animal instanceof Dog) {
      ((Dog) animal).walk();
    } else if (animal instanceof Cat) {
      ((Cat) animal).cleanLitterBox();
    }
 
    throw new Exception("Not sure how to handle " + animal);
  }
}

I've just realized that I can't exhaustively handle all the cases for HousePet since it's always open to be implemented. So instead I throw an error. This works great! I know the only two cases that are HousePets are Dog and Cat, so I shouldn't have to worry about the exception being thrown, right?

A wrench thrown into the works#

Well, a user of my library decides to implement HousePet for their own Animal variant:

record Snake(String name, int age, String sound) implements HousePet {
  public Snake(String name, int age) {
    this(name, age, "Hiss");
  }
 
  public void shedSkin() {
    System.out.println("Shedding skin for " + this.name());
  }
}

When they call takeCareOfHousePets they get an exception thrown. This is because I didn't handle the case for Snake in my takeCareOfHousePets method.

// Exception: Not sure how to handle Snake[name=Sneaky, age=1, sound=Hiss]
takeCareOfHousePets(new List<>(new Dog("Fido", 3), new Cat("Garfield", 5), new Snake("Sneaky", 1)));

My code wasn't designed for people to add their own variants. However, due to the nature of access-control and interfaces, they can. Many jaded java developers would simply accept throwing an exception as a valid solution to this problem. However, exception throwing is a last resort. It's a hack to get around the fact that you can't exhaustively match on a product type. A more elegant solution could be validate this kind of error at compile-time.

This is where sum types come to the rescue.

Sum types to the rescue#

In earlier versions of java the concept of a sum type was essentially using an enum with an associated value: We would remodel our code above to this:

public enum HousePet {
  DOG(new Dog()),
  CAT(new Cat()),
 
  constructor (Animal animal) {
    this.animal = animal;
  }
}

Let's look at how we can handle this sum type:

void takeCareOfHousePets(List<HousePet> animals) {
  for (HousePet animalVariant : animals) {
    switch (animal) {
      case DOG -> animalVariant.animal.walk();
      case CAT -> animalVariant.animal.cleanLitterBox();
    }
  }
}

Notice that we don't need a default case in our switch statement. This is because we've exhaustively matched on all the variants of HousePet. This is core benefit of sum types. We can be sure that we've handled all the cases. The type cannot contain any extra variants beyond the ones we've defined.

Modern Java makes sum types easier#

You may have noticed that the enum approach introduces an unwanted level of indirection. Modern versions of java introduce the concept of sealed types. This allows us to define our sum type like so:

public sealed interface HousePet extends Animal permits Dog, Cat {
  default void takeCareOf() {
    System.out.println("Taking care of " + this.name());
  }
}

This is a lot cleaner than the enum approach. We can now define our variants like we originally did:

public final record Dog(String name, int age, String sound) implements HousePet { ... }
public final record Cat(String name, int age, String sound) implements HousePet { ... }

Let's say our user decides to implement HousePet for their own Animal variant:

public final record Snake(String name, int age, String sound) implements HousePet {
  ...
}
 
// Error: Cannot implement `HousePet`, `Snake` is not a permitted type

The type is now closed for extension and we get a nice compile-time error.

We can guarantee that we've handled all the cases for sealed classes like HousePet by pattern matching instanceof:

void takeCareOfHousePets(List<HousePet> animals) {
  for (HousePet animal : animals) {
    switch (animal) {
      case Dog dog -> dog.walk();
      case Cat cat -> cat.cleanLitterBox();
    }
  }
}

Other languages#

The world of programming is made up of more than just java. Other languages have their own ways of handling sum types. Let's look at a few of them.

Rust#

Rust takes a similar approach to java with the concept of enums and associated values:

enum HousePet {
  Dog(Dog),
  Cat(Cat),
}

Unlike Java, rust enum members can hold types that aren't covariant to other enum members. This means theoretically would could have a Person(Person) variant in the HousePet struct, even though a Person isn't compatible to a HousePet. This behaviour allows rust enums to be more flexible than java enums in some instances.

Haskell#

In terms of syntax, Haskell takes a different approach to sum types. It uses the | (union) operator to define variants:

data HousePet = Dog Dog | Cat Cat

Similar to rust, each variant can be disjoint from the others.

Typescript#

Typescript is similiar to haskell syntax-wise but uses types as-is rather than wrapping them in distinct named variants:

type HousePet = Dog | Cat;

Because sum types in typescript don't have nominal labels, you can't match on them directly like you do in haskell or rust. Instead you need to use instanceof checks against the types:

function takeCareOfHousePets(animals: HousePet[]) {
	for (const animal of animals) {
		if (animal instanceof Dog) {
			animal.walk();
		} else if (animal instanceof Cat) {
			animal.cleanLitterBox();
		}
	}
}

However, this doesn't cover cases where objects are used instead of classes. We can't check instanceof on objects. So we need to use a different approach. We can use something called a "discriminant property" to identify the type of the object. This is a property that is unique to each variant. For example, we could add a type to each variant:

type Dog = {
	type: "dog";
	name: string;
	age: number;
	sound: string;
};
 
type Cat = {
	type: "cat";
	name: string;
	age: number;
	sound: string;
};
 
type HousePet = Dog | Cat;

Now we can disambiguate HousePet objects by checking the type property:

function takeCareOfHousePets(animals: HousePet[]) {
	for (const animal of animals) {
		if (animal.type === "dog") {
			animal.walk();
		} else if (animal.type === "cat") {
			animal.cleanLitterBox();
		}
	}
}

Conclusion#

I should make it clear that polymorphic types are not useless by any means. Both sum types and polymorphic types are two different ways of modeling two different types of data.

For reference:

• When you have a type that is meant to be implemented, or is used to show a contract is satisfied. Use polymorphic types to model this. For example, if you want to model shapes, you can introduce an interface with a getArea() method. This allows you introduce new shapes under the Shape type umbrella.
• When you have a limited set of variants that may or may not be covariant with each other. Use sum types to model this. See our HousePet example above.